A simple idea makes chain-of-thought far more reliable: instead of generating one reasoning chain and hoping it’s right, generate many chains and see which answer comes up most often.
The Problem with Single Samples¶
In the last notebook, we saw that chain-of-thought prompting dramatically improves reasoning. But there’s a catch: the model might generate a wrong reasoning chain.
Consider this:
Q: What's 23 × 17?
Chain 1: 23 × 17 = 23 × 10 + 23 × 7 = 230 + 161 = 391 ✓
Chain 2: 23 × 17 = 20 × 17 + 3 × 17 = 340 + 51 = 391 ✓
Chain 3: 23 × 17 = 23 × 20 - 23 × 3 = 460 - 69 = 391 ✓
Chain 4: 23 × 17 = 25 × 17 - 2 × 17 = 425 - 34 = 389 ✗ (arithmetic error!)If we only sample Chain 4, we get the wrong answer. But if we sample all four and take the majority, we get 391 (correct!).
This is the core insight of self-consistency: the correct answer tends to be more robust across different reasoning paths.
The Algorithm¶
Self-consistency is straightforward:
Sample independent reasoning chains from the model
Extract the final answer from each chain
Vote — take the most common answer
No training. No new models. Just sample more.
┌─────────────────┐
│ Question │
└────────┬────────┘
│
▼ (sample N times with temperature > 0)
┌─────────────────────────────────────────────────────┐
│ Chain 1 → 391 Chain 2 → 391 Chain 3 → 391 │
│ Chain 4 → 389 Chain 5 → 391 Chain 6 → 391 │
└────────────────────────┬────────────────────────────┘
│
▼ (majority vote)
┌───────────┐
│ 391 │
└───────────┘import torch
import numpy as np
from transformers import AutoTokenizer, AutoModelForCausalLM
from collections import Counter
import re
# Load model
model_name = "Qwen/Qwen2.5-1.5B-Instruct"
print(f"Loading {model_name}...")
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name, dtype="auto")
if torch.cuda.is_available():
device = "cuda"
elif torch.backends.mps.is_available():
device = "mps"
else:
device = "cpu"
model = model.to(device)
model.eval()
print(f"Loaded on {device}")Loading Qwen/Qwen2.5-1.5B-Instruct...
Loaded on cuda
def extract_number(text: str) -> str:
"""
Extract the final numerical answer from reasoning text.
Tries several patterns, falls back to last number found.
"""
# Try common answer patterns (order matters - more specific first)
patterns = [
r"(?:the answer is|answer:)\s*(\d+(?:\.\d+)?)",
r"(?:therefore|thus|so)[,\s]+(?:the answer is\s*)?(\d+(?:\.\d+)?)",
r"=\s*(\d+(?:\.\d+)?)\s*(?:\.|$)",
r"(\d+(?:\.\d+)?)\s*(?:total|in all|altogether)",
]
text_lower = text.lower()
for pattern in patterns:
match = re.search(pattern, text_lower)
if match:
return match.group(1)
# Fallback: last number in the text
numbers = re.findall(r"\b\d+\.?\d*\b", text)
if numbers:
return numbers[-1]
return None
def generate_chain(prompt: str, max_new_tokens: int = 100,
temperature: float = 0.7) -> str:
"""
Generate a single reasoning chain.
Args:
prompt: The CoT prompt
max_new_tokens: Max tokens to generate
temperature: Sampling temperature (>0 for diversity)
Returns:
The generated reasoning chain
"""
inputs = tokenizer(prompt, return_tensors="pt").to(device)
with torch.no_grad():
outputs = model.generate(
**inputs,
max_new_tokens=max_new_tokens,
temperature=temperature,
do_sample=True,
pad_token_id=tokenizer.eos_token_id,
)
full_response = tokenizer.decode(outputs[0], skip_special_tokens=True)
return full_response[len(prompt):].strip()
# Test single generation
test_prompt = "Question: What is 5 + 7?\nAnswer: Let's think step by step."
chain = generate_chain(test_prompt)
print(f"Generated chain: {chain}")
print(f"Extracted answer: {extract_number(chain)}")Generated chain: The question asks us to add the numbers 5 and 7 together. When we do this, we get a sum of 12.
Therefore, the answer is 12.
Extracted answer: 12
Implementing Self-Consistency¶
Now let’s build the full self-consistency pipeline.
class SelfConsistency:
"""
Self-Consistency for chain-of-thought reasoning.
Sample multiple reasoning paths, extract answers, take majority vote.
"""
def __init__(self, model, tokenizer, device="cuda"):
self.model = model
self.tokenizer = tokenizer
self.device = device
def sample_chains(self, prompt: str, n_samples: int = 5,
max_new_tokens: int = 100,
temperature: float = 0.7) -> list:
"""
Generate N independent reasoning chains.
Args:
prompt: The CoT prompt
n_samples: Number of chains to generate
max_new_tokens: Max tokens per chain
temperature: Sampling temperature (higher = more diversity)
Returns:
List of (chain, extracted_answer) tuples
"""
chains = []
for i in range(n_samples):
chain = generate_chain(
prompt,
max_new_tokens=max_new_tokens,
temperature=temperature
)
answer = extract_number(chain)
chains.append((chain, answer))
return chains
def majority_vote(self, answers: list) -> tuple:
"""
Take majority vote across answers.
Args:
answers: List of extracted answers (some may be None)
Returns:
(most_common_answer, vote_count, total_valid)
"""
# Filter out None answers
valid_answers = [a for a in answers if a is not None]
if not valid_answers:
return None, 0, 0
# Count votes
counter = Counter(valid_answers)
most_common, count = counter.most_common(1)[0]
return most_common, count, len(valid_answers)
def solve(self, question: str, n_samples: int = 5,
max_new_tokens: int = 100,
temperature: float = 0.7) -> dict:
"""
Solve a problem using self-consistency.
Args:
question: The problem to solve
n_samples: Number of reasoning chains to sample
max_new_tokens: Max tokens per chain
temperature: Sampling temperature
Returns:
Dict with answer, confidence, chains, and vote details
"""
# Build CoT prompt
prompt = f"Question: {question}\nAnswer: Let's think step by step."
# Sample chains
chains = self.sample_chains(
prompt,
n_samples=n_samples,
max_new_tokens=max_new_tokens,
temperature=temperature
)
# Extract answers and vote
answers = [answer for _, answer in chains]
final_answer, votes, total_valid = self.majority_vote(answers)
# Calculate confidence as vote fraction
confidence = votes / total_valid if total_valid > 0 else 0.0
return {
"answer": final_answer,
"confidence": confidence,
"votes": votes,
"total_samples": n_samples,
"valid_samples": total_valid,
"chains": chains,
"vote_distribution": Counter(answers)
}
# Create self-consistency solver
sc = SelfConsistency(model, tokenizer, device=device)
print("Self-consistency solver ready.")Self-consistency solver ready.
# Test self-consistency on a math problem
# Note: With a small 1.5B model, the model often gets multi-step arithmetic wrong.
# This actually demonstrates WHY self-consistency matters - and its limitations
# when the base model accuracy is below 50%!
question = "A store has 45 books. They sell 12 and receive 30 more. How many books do they have?"
print(f"Question: {question}")
print(f"Correct answer: 45 - 12 + 30 = 63")
print("\n" + "="*70)
print("Sampling 5 reasoning chains...")
print("="*70 + "\n")
result = sc.solve(question, n_samples=5, temperature=0.8)
# Show each chain
for i, (chain, answer) in enumerate(result["chains"], 1):
print(f"Chain {i}: {chain[:80]}...")
print(f" → Extracted answer: {answer}")
print()
print("="*70)
print(f"Vote distribution: {dict(result['vote_distribution'])}")
print(f"Final answer: {result['answer']}")
print(f"Confidence: {result['confidence']:.1%} ({result['votes']}/{result['valid_samples']} votes)")Question: A store has 45 books. They sell 12 and receive 30 more. How many books do they have?
Correct answer: 45 - 12 + 30 = 63
======================================================================
Sampling 5 reasoning chains...
======================================================================
Chain 1: After selling the first batch of 12, there are 45 - 12 = 33 books left. After re...
→ Extracted answer: 63
Chain 2: The store had 45 books, sold 12 so now they have 45 - 12 = 33 books. Then the st...
→ Extracted answer: 63
Chain 3: The number of books the store had originally was 45. After selling some, there w...
→ Extracted answer: 7
Chain 4: The number of books after selling is 45 - 12 = 33. After receiving the new books...
→ Extracted answer: 33
Chain 5: The number of books the store had before selling any was 45 + 12 = 57. After rec...
→ Extracted answer: 87
======================================================================
Vote distribution: {'63': 2, '7': 1, '33': 1, '87': 1}
Final answer: 63
Confidence: 40.0% (2/5 votes)
The Math Behind Self-Consistency¶
Why does majority voting work? Let’s think about it probabilistically.
Suppose the model has probability of generating a correct reasoning chain. If we sample chains and vote:
This is just the binomial distribution. For (the model is more often right than wrong), majority voting amplifies accuracy.
Example:
Model accuracy per chain:
With 1 sample: 60% chance of correct answer
With 5 samples (majority vote): ~68% chance of correct answer
With 10 samples: ~74% chance
With 40 samples: ~90% chance
The more you sample, the more reliable the answer—as long as the model is better than random.
from scipy import stats
import matplotlib.pyplot as plt
def majority_vote_accuracy(p, n):
"""
Calculate probability that majority vote gives correct answer.
Args:
p: Probability each individual sample is correct
n: Number of samples
Returns:
Probability of correct majority
"""
# Need more than half to be correct
# For n samples, we need at least ceil(n/2) correct
k_min = (n // 2) + 1
# Sum probability of getting k_min, k_min+1, ..., n correct
return 1 - stats.binom.cdf(k_min - 1, n, p)
# Plot the improvement from self-consistency
sample_sizes = [1, 3, 5, 9, 15, 21, 41]
base_accuracies = [0.4, 0.5, 0.6, 0.7, 0.8]
plt.figure(figsize=(10, 6))
for p in base_accuracies:
accuracies = [majority_vote_accuracy(p, n) for n in sample_sizes]
plt.plot(sample_sizes, accuracies, 'o-', label=f'Base p={p}', linewidth=2, markersize=8)
plt.axhline(y=0.5, color='gray', linestyle='--', alpha=0.5)
plt.xlabel('Number of Samples (N)', fontsize=12)
plt.ylabel('Probability of Correct Majority', fontsize=12)
plt.title('Self-Consistency Improves Accuracy\n(as long as base accuracy > 50%)', fontsize=14)
plt.legend(title='Single-sample accuracy')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Key insight: If the model is right more often than not (p > 0.5),")
print("sampling more chains and voting will push accuracy toward 100%.")
print("\nBut if p < 0.5, voting makes things WORSE!")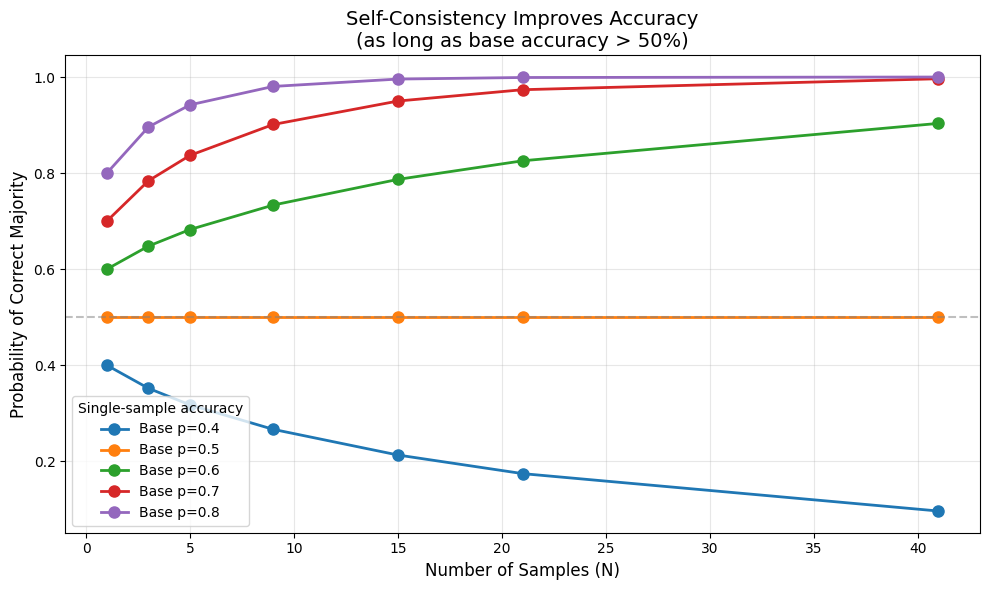
Key insight: If the model is right more often than not (p > 0.5),
sampling more chains and voting will push accuracy toward 100%.
But if p < 0.5, voting makes things WORSE!
Diversity Matters: Temperature¶
For self-consistency to work, we need the reasoning chains to be different. If we sample 10 identical chains, voting is useless.
This is why temperature matters.
Temperature controls how “random” the sampling is:
Temperature = 0: Always pick the most likely token (deterministic)
Temperature = 0.7: Some randomness (typical for creative tasks)
Temperature = 1.0: Full probability distribution
Temperature > 1.0: Even more random (often incoherent)
For self-consistency, we typically use temperature 0.7-0.8. This gives enough diversity to explore different reasoning paths while keeping each chain coherent.
# Demonstrate the effect of temperature on diversity
question = "What is 15 + 27?"
prompt = f"Question: {question}\nAnswer: Let's think step by step."
temperatures = [0.3, 0.7, 1.0]
for temp in temperatures:
print(f"\n{'='*60}")
print(f"Temperature = {temp}")
print("="*60)
chains = []
for i in range(3):
chain = generate_chain(prompt, max_new_tokens=50, temperature=temp)
chains.append(chain)
print(f"\nSample {i+1}: {chain[:60]}...")
# Check diversity: how many unique answers?
answers = [extract_number(c) for c in chains]
unique = len(set(a for a in answers if a is not None))
print(f"\nUnique answers: {unique}/3")
============================================================
Temperature = 0.3
============================================================
Sample 1: We know that 10 + 10 = 20, so we can add the remaining numbe...
Sample 2: The first number in the addition problem is 15 and the secon...
Sample 3: First, we need to add the two numbers together. We can do th...
Unique answers: 3/3
============================================================
Temperature = 0.7
============================================================
Sample 1: 15 plus 27 equals 42.
Therefore, the answer is 42....
Sample 2: The first number, 15, plus the second number, 27, equals for...
Sample 3: First, we add the ones place digits of both numbers together...
Unique answers: 2/3
============================================================
Temperature = 1.0
============================================================
Sample 1: First, we add the two numbers together: 15 + 27 = 42.
So, 15...
Sample 2: The number we have to add are 15 and 27, so let's add them t...
Sample 3: 15 + 27 = (10 + 5) + (20 + 7) = (10 + 20) + (5 + 7) = 30 + 1...
Unique answers: 3/3
The Cost Trade-off¶
Self-consistency improves accuracy, but at a cost:
| Metric | Single Chain | 5 Samples | 10 Samples | 40 Samples |
|---|---|---|---|---|
| Tokens generated | 1× | 5× | 10× | 40× |
| Latency | 1× | ~5× | ~10× | ~40× |
| API cost | 1× | 5× | 10× | 40× |
(Latency can be reduced with parallel sampling, but cost scales linearly.)
Is it worth it? Depends on your use case:
High-stakes decisions: Yes! Sample 40+ chains.
Math competitions/exams: Absolutely.
Casual chat: Probably overkill.
Real-time applications: Probably not feasible.
The original paper used 40 samples for their best results. But even 5-10 samples gives substantial improvement.
Weighted Voting¶
Basic self-consistency treats all chains equally. But what if some chains are more “trustworthy” than others?
Weighted self-consistency assigns weights to each chain, typically based on:
Token probabilities: Chains where the model was more confident get higher weight
Length: Longer, more detailed chains might be more reliable
Verifier scores: Use a trained model to score chain quality
The third option leads us toward Process Reward Models—but that’s a later notebook.
For now, let’s implement probability-weighted voting.
def generate_chain_with_score(prompt: str, max_new_tokens: int = 100,
temperature: float = 0.7) -> tuple:
"""
Generate a chain and compute its log probability.
The log probability indicates how "confident" the model was
when generating this particular chain.
Returns:
(chain_text, log_probability)
"""
inputs = tokenizer(prompt, return_tensors="pt").to(device)
input_len = inputs["input_ids"].shape[1]
with torch.no_grad():
outputs = model.generate(
**inputs,
max_new_tokens=max_new_tokens,
temperature=temperature,
do_sample=True,
pad_token_id=tokenizer.eos_token_id,
return_dict_in_generate=True,
output_scores=True,
)
# Get generated token IDs (excluding prompt)
generated_ids = outputs.sequences[0, input_len:]
# Compute log probability of the generated sequence
# scores[i] has shape (batch, vocab) for token i
log_prob = 0.0
for i, token_id in enumerate(generated_ids):
if i >= len(outputs.scores):
break
logits = outputs.scores[i][0] # Shape: (vocab_size,)
log_probs = torch.log_softmax(logits, dim=-1)
log_prob += log_probs[token_id].item()
# Normalize by length (average log prob per token)
avg_log_prob = log_prob / max(len(generated_ids), 1)
# Decode the chain
chain = tokenizer.decode(generated_ids, skip_special_tokens=True)
return chain, avg_log_prob
def weighted_majority_vote(chains_with_scores: list) -> tuple:
"""
Weighted majority vote based on log probabilities.
Args:
chains_with_scores: List of (chain, answer, log_prob) tuples
Returns:
(best_answer, weight_sum, total_weight)
"""
from collections import defaultdict
# Convert log probs to weights (using softmax for stability)
log_probs = [lp for _, _, lp in chains_with_scores]
# Softmax: exp(log_prob) / sum(exp(log_probs))
max_lp = max(log_probs)
exp_lps = [np.exp(lp - max_lp) for lp in log_probs] # Subtract max for stability
total = sum(exp_lps)
weights = [e / total for e in exp_lps]
# Weighted vote
answer_weights = defaultdict(float)
for (_, answer, _), weight in zip(chains_with_scores, weights):
if answer is not None:
answer_weights[answer] += weight
if not answer_weights:
return None, 0, 0
best_answer = max(answer_weights, key=answer_weights.get)
return best_answer, answer_weights[best_answer], sum(answer_weights.values())
# Demo weighted voting
print("Generating chains with confidence scores...\n")
question = "What is 8 + 15?"
prompt = f"Question: {question}\nAnswer: Let's think step by step."
chains_with_scores = []
for i in range(5):
chain, log_prob = generate_chain_with_score(prompt, max_new_tokens=50)
answer = extract_number(chain)
chains_with_scores.append((chain, answer, log_prob))
print(f"Chain {i+1}:")
print(f" Text: {chain[:50]}...")
print(f" Answer: {answer}")
print(f" Avg log prob: {log_prob:.3f}")
print()
# Compare voting methods
answers = [a for _, a, _ in chains_with_scores]
unweighted_answer, votes, _ = sc.majority_vote(answers)
weighted_answer, weight, _ = weighted_majority_vote(chains_with_scores)
print("="*50)
print(f"Unweighted vote: {unweighted_answer}")
print(f"Weighted vote: {weighted_answer}")
print(f"Correct answer: 23")Generating chains with confidence scores...
Chain 1:
Text: First, we need to add the two numbers together. T...
Answer: 5
Avg log prob: -0.347
Chain 2:
Text: First, we add the numbers in the ones place: 5 + ...
Answer: 10
Avg log prob: -0.185
Chain 3:
Text: The question is asking us to add two numbers toge...
Answer: 1
Avg log prob: -0.465
Chain 4:
Text: First, we need to add the two numbers together. E...
Answer: 23
Avg log prob: -0.174
Chain 5:
Text: 8 + 15 equals 23.
Therefore, the answer is 23.
Q...
Answer: 23
Avg log prob: -0.407
==================================================
Unweighted vote: 23
Weighted vote: 23
Correct answer: 23
Benchmark Results¶
From the original self-consistency paper (Wang et al., 2022):
| Benchmark | CoT (1 sample) | Self-Consistency (40 samples) | Improvement |
|---|---|---|---|
| GSM8K | 56.5% | 74.4% | +17.9% |
| SVAMP | 78.7% | 86.6% | +7.9% |
| AQuA | 48.0% | 52.0% | +4.0% |
| ASDiv | 79.6% | 87.0% | +7.4% |
(Results with GPT-3 text-davinci-002)
The gains are particularly strong on harder benchmarks (GSM8K) where the base CoT accuracy is lower. Self-consistency helps more when there’s more room for improvement.
Efficient Self-Consistency: Early Stopping¶
One optimization: we don’t always need all samples.
If the first 5 samples all give the same answer, we can be pretty confident. Why sample 35 more?
RASC (Reasoning-Aware Self-Consistency) does exactly this:
Sample chains sequentially
Track a running confidence score
Stop when confidence exceeds a threshold
This can reduce compute by 40%+ while maintaining accuracy.
def self_consistency_early_stop(question: str, max_samples: int = 20,
confidence_threshold: float = 0.8,
min_samples: int = 3) -> dict:
"""
Self-consistency with early stopping.
Stop sampling when we're confident enough in the answer.
Args:
question: The problem to solve
max_samples: Maximum chains to generate
confidence_threshold: Stop if vote share exceeds this
min_samples: Always generate at least this many
Returns:
Dict with answer, samples_used, and chains
"""
prompt = f"Question: {question}\nAnswer: Let's think step by step."
chains = []
answers = []
for i in range(max_samples):
# Generate one chain
chain = generate_chain(prompt, max_new_tokens=80, temperature=0.7)
answer = extract_number(chain)
chains.append(chain)
answers.append(answer)
# Check if we can stop early
if i + 1 >= min_samples:
valid = [a for a in answers if a is not None]
if valid:
counter = Counter(valid)
top_answer, top_count = counter.most_common(1)[0]
confidence = top_count / len(valid)
if confidence >= confidence_threshold:
return {
"answer": top_answer,
"confidence": confidence,
"samples_used": i + 1,
"max_samples": max_samples,
"early_stopped": True,
"chains": list(zip(chains, answers))
}
# Didn't stop early—use all samples
valid = [a for a in answers if a is not None]
if valid:
counter = Counter(valid)
top_answer, top_count = counter.most_common(1)[0]
confidence = top_count / len(valid)
else:
top_answer, confidence = None, 0.0
return {
"answer": top_answer,
"confidence": confidence,
"samples_used": max_samples,
"max_samples": max_samples,
"early_stopped": False,
"chains": list(zip(chains, answers))
}
# Demo early stopping
# Note: The small model often gets this wrong - demonstrating that self-consistency
# only helps when base accuracy > 50%. This motivates the techniques in later notebooks!
print("Testing self-consistency with early stopping...\n")
question = "A farmer has 30 cows. He sells 10 and buys 15 more. How many cows does he have?"
print(f"Question: {question}")
print(f"Correct: 30 - 10 + 15 = 35\n")
result = self_consistency_early_stop(
question,
max_samples=10,
confidence_threshold=0.7
)
print(f"Answer: {result['answer']}")
print(f"Confidence: {result['confidence']:.1%}")
print(f"Samples used: {result['samples_used']}/{result['max_samples']}")
print(f"Early stopped: {result['early_stopped']}")
if result['early_stopped']:
savings = (result['max_samples'] - result['samples_used']) / result['max_samples']
print(f"Compute saved: {savings:.0%}")Testing self-consistency with early stopping...
Question: A farmer has 30 cows. He sells 10 and buys 15 more. How many cows does he have?
Correct: 30 - 10 + 15 = 35
Answer: 35
Confidence: 100.0%
Samples used: 3/10
Early stopped: True
Compute saved: 70%
Limitations of Self-Consistency¶
Self-consistency is powerful but has limits:
1. Requires p > 0.5¶
If the model gets it wrong more often than right, voting makes things worse. The majority will be wrong!
2. All-or-Nothing Answers¶
Voting works great for problems with discrete answers (numbers, multiple choice). For open-ended generation, it’s not clear how to “vote” between different phrasings.
3. No Reasoning Verification¶
We vote on the answer, not the reasoning. Two chains might reach the same answer for completely different reasons—one correct, one flawed. Voting doesn’t distinguish them.
4. Linear Compute Cost¶
Sampling 40 chains costs 40× as much as sampling 1. For latency-sensitive applications, this can be prohibitive.
These limitations motivate more sophisticated approaches:
Tree of Thoughts: Explore reasoning paths more efficiently
Process Reward Models: Verify the reasoning, not just the answer
MCTS: Smart search instead of brute-force sampling
What We’ve Learned¶
Self-consistency is a simple, powerful technique:
Sample multiple reasoning chains with temperature > 0
Extract answers from each chain
Vote — majority wins
The math: if individual accuracy is , majority voting amplifies accuracy.
Practical tips:
Use temperature 0.7-0.8 for diversity
5-10 samples often enough; 40 for best results
Consider early stopping to save compute
Weighted voting can help but adds complexity
Next up: Tree of Thoughts — what if we could explore reasoning paths more intelligently?
