Best-of-N generates solutions independently. Tree of Thoughts explores a tree but uses simple heuristics. MCTS combines the best of both: systematic tree exploration guided by learned value estimates.
This is how AlphaGo beat the world champion at Go. And it’s how some of the best reasoning systems work today.
The Core Idea¶
MCTS builds a search tree through repeated simulations. Each simulation has four phases:
┌─────────────────────────────────────────────────────────────────┐
│ 1. SELECT │
│ Start at root, use UCB formula to pick child nodes │
│ until reaching an unexplored node │
└─────────────────────────────────────────────────────────────────┘
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ 2. EXPAND │
│ Add child nodes for possible next steps │
└─────────────────────────────────────────────────────────────────┘
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ 3. SIMULATE (Rollout) │
│ Play out to the end (or use value estimate) │
└─────────────────────────────────────────────────────────────────┘
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ 4. BACKPROPAGATE │
│ Update value estimates along the path │
└─────────────────────────────────────────────────────────────────┘Repeat many times, then pick the most-visited (or highest-value) action.
The UCB Formula¶
The core of MCTS is the Upper Confidence Bound (UCB) formula for selecting which branch to explore:
Where:
= Average value of taking action in state
= Number of times we’ve visited state
= Number of times we’ve taken action from state
= Exploration constant (balances exploration vs. exploitation)
The first term favors exploitation (actions that worked well before). The second term favors exploration (actions we haven’t tried much).
As increases, the exploration bonus shrinks. Eventually, focus shifts to the best actions.
import torch
from transformers import AutoTokenizer, AutoModelForCausalLM
from dataclasses import dataclass, field
from typing import List, Dict, Optional, Callable
import numpy as np
import math
import matplotlib.pyplot as plt
# Load model
model_name = "Qwen/Qwen2.5-0.5B-Instruct"
print(f"Loading {model_name}...")
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModelForCausalLM.from_pretrained(model_name, dtype="auto")
if torch.cuda.is_available():
device = "cuda"
elif torch.backends.mps.is_available():
device = "mps"
else:
device = "cpu"
model = model.to(device)
model.eval()
print(f"Loaded on {device}")Loading Qwen/Qwen2.5-0.5B-Instruct...
Loaded on cuda
@dataclass
class MCTSNode:
"""
A node in the MCTS tree.
"""
state: str # The reasoning state so far
thought: str = "" # The thought that led here
parent: Optional['MCTSNode'] = None
children: Dict[str, 'MCTSNode'] = field(default_factory=dict)
# MCTS statistics
visits: int = 0
value_sum: float = 0.0
@property
def value(self) -> float:
"""Average value (Q-value)."""
if self.visits == 0:
return 0.0
return self.value_sum / self.visits
def ucb_score(self, c: float = 1.41) -> float:
"""
Compute UCB score for this node.
c=1.41 ≈ sqrt(2) is a common default.
"""
if self.visits == 0:
return float('inf') # Unexplored = infinite priority
if self.parent is None:
return self.value
exploitation = self.value
exploration = c * math.sqrt(math.log(self.parent.visits) / self.visits)
return exploitation + exploration
def is_leaf(self) -> bool:
return len(self.children) == 0
def best_child(self, c: float = 1.41) -> 'MCTSNode':
"""Select child with highest UCB score."""
return max(self.children.values(), key=lambda n: n.ucb_score(c))
def most_visited_child(self) -> 'MCTSNode':
"""Select most-visited child (for final action selection)."""
return max(self.children.values(), key=lambda n: n.visits)
print("MCTSNode defined.")MCTSNode defined.
def generate_thoughts(state: str, n: int = 3, temperature: float = 0.8) -> List[str]:
"""
Generate n possible next thoughts from a state.
"""
prompt = f"{state}\n\nWhat is a good next step? Respond with just the next step:"
thoughts = []
inputs = tokenizer(prompt, return_tensors="pt").to(device)
for _ in range(n):
with torch.no_grad():
outputs = model.generate(
**inputs,
max_new_tokens=50,
temperature=temperature,
do_sample=True,
pad_token_id=tokenizer.eos_token_id,
)
text = tokenizer.decode(outputs[0], skip_special_tokens=True)
thought = text[len(prompt):].strip().split('\n')[0]
if thought and thought not in thoughts:
thoughts.append(thought)
return thoughts
def evaluate_state(state: str) -> float:
"""
Evaluate a reasoning state (simple heuristic).
In practice, you'd use a trained value network or PRM.
"""
score = 0.5
# Reward step-by-step reasoning
if 'step' in state.lower():
score += 0.1
# Reward calculations
import re
if re.search(r'\d+\s*[+\-*/]\s*\d+\s*=', state):
score += 0.2
# Reward final answer
if 'answer' in state.lower():
score += 0.1
return min(1.0, score)
# Test
test_state = "Problem: What is 5 + 3?\nLet me think step by step."
thoughts = generate_thoughts(test_state, n=3)
print("Generated thoughts:")
for i, t in enumerate(thoughts, 1):
print(f" {i}. {t}")Generated thoughts:
1. The sum of two numbers, 5 and 3, can be calculated by adding them together.
2. To find the sum of 5 and 3, I need to add them together. How do you add numbers?
3. To find the sum of five and three, we can add the numbers together.
class MCTS:
"""
Monte Carlo Tree Search for language model reasoning.
"""
def __init__(self, expand_fn: Callable, evaluate_fn: Callable,
c: float = 1.41, max_depth: int = 5):
self.expand_fn = expand_fn # Generate possible next thoughts
self.evaluate_fn = evaluate_fn # Evaluate a state
self.c = c # Exploration constant
self.max_depth = max_depth
def select(self, node: MCTSNode) -> MCTSNode:
"""
Phase 1: Select a leaf node using UCB.
"""
current = node
depth = 0
while not current.is_leaf() and depth < self.max_depth:
current = current.best_child(self.c)
depth += 1
return current
def expand(self, node: MCTSNode, n_children: int = 3) -> MCTSNode:
"""
Phase 2: Expand by adding child nodes.
"""
if node.visits == 0:
# First visit — just return the node to evaluate
return node
# Generate possible next thoughts
thoughts = self.expand_fn(node.state, n=n_children)
for thought in thoughts:
if thought not in node.children:
new_state = f"{node.state}\n{thought}"
child = MCTSNode(
state=new_state,
thought=thought,
parent=node
)
node.children[thought] = child
# Return a random new child to evaluate
if node.children:
unvisited = [c for c in node.children.values() if c.visits == 0]
if unvisited:
return np.random.choice(unvisited)
return node.best_child(self.c)
return node
def simulate(self, node: MCTSNode) -> float:
"""
Phase 3: Evaluate the node (or rollout).
In classic MCTS, this plays random moves to terminal state.
With LLMs, we typically just use a value estimate.
"""
return self.evaluate_fn(node.state)
def backpropagate(self, node: MCTSNode, value: float):
"""
Phase 4: Update values along the path to root.
"""
current = node
while current is not None:
current.visits += 1
current.value_sum += value
current = current.parent
def search(self, root: MCTSNode, n_simulations: int = 50) -> MCTSNode:
"""
Run MCTS for n_simulations and return best node.
"""
for i in range(n_simulations):
# 1. Select
leaf = self.select(root)
# 2. Expand
node = self.expand(leaf)
# 3. Simulate
value = self.simulate(node)
# 4. Backpropagate
self.backpropagate(node, value)
return root.most_visited_child() if root.children else root
def solve(self, problem: str, n_simulations: int = 50,
n_steps: int = 3) -> dict:
"""
Solve a problem using MCTS.
"""
# Initialize root
root = MCTSNode(
state=f"Problem: {problem}\nLet me solve this step by step."
)
# Build solution step by step
current = root
path = []
for step in range(n_steps):
# Run MCTS from current node
best = self.search(current, n_simulations=n_simulations)
if best.thought:
path.append(best.thought)
current = best
# Check if we've reached an answer
if 'answer' in current.state.lower():
break
return {
"solution": current.state,
"path": path,
"value": current.value,
"visits": current.visits,
"root": root
}
# Create MCTS solver
mcts = MCTS(
expand_fn=generate_thoughts,
evaluate_fn=evaluate_state,
c=1.41,
max_depth=5
)
print("MCTS solver ready.")MCTS solver ready.
# Test MCTS
problem = "What is 12 + 8?"
print(f"Problem: {problem}")
print(f"Correct: 20")
print("\n" + "="*60)
print("Running MCTS...")
result = mcts.solve(problem, n_simulations=20, n_steps=3)
print("\n" + "="*60)
print("SOLUTION PATH:")
print("="*60)
for i, step in enumerate(result['path'], 1):
print(f"Step {i}: {step}")
print(f"\nFinal value: {result['value']:.3f}")
print(f"Total visits: {result['visits']}")Problem: What is 12 + 8?
Correct: 20
============================================================
Running MCTS...
============================================================
SOLUTION PATH:
============================================================
Step 1: Next, find a place to write down the answer.
Final value: 0.700
Total visits: 7
Visualizing the Search Tree¶
One of the nice things about MCTS is that we can visualize what it explored.
def print_tree(node: MCTSNode, indent: int = 0, max_depth: int = 3):
"""
Print the MCTS tree structure.
"""
if indent > max_depth * 2:
return
prefix = " " * indent
thought_preview = node.thought[:40] + "..." if len(node.thought) > 40 else node.thought
if node.thought:
print(f"{prefix}├─ {thought_preview}")
print(f"{prefix}│ visits={node.visits}, value={node.value:.2f}, ucb={node.ucb_score():.2f}")
else:
print(f"{prefix}[ROOT] visits={node.visits}")
for child in sorted(node.children.values(), key=lambda n: -n.visits):
print_tree(child, indent + 1, max_depth)
print("MCTS Search Tree:")
print("="*60)
print_tree(result['root'], max_depth=2)MCTS Search Tree:
============================================================
[ROOT] visits=20
├─ Next, find a place to write down the ans...
│ visits=7, value=0.70, ucb=1.62
├─ Next, let's add the numbers.
│ visits=2, value=0.70, ucb=2.09
├─ Next, let's add the numbers.
│ visits=1, value=0.70, ucb=1.87
├─ Find a place to write down the answer.
│ visits=0, value=0.00, ucb=inf
├─ Next, write down the sum. So the final a...
│ visits=2, value=0.70, ucb=2.09
├─ Next, write down the sum of the two numb...
│ visits=1, value=0.70, ucb=1.87
├─ The first thing you should do after find...
│ visits=0, value=0.00, ucb=inf
├─ The final answer is 20. What is a good n...
│ visits=0, value=0.00, ucb=inf
├─ Next, we need to add 12 and 8. Let's do ...
│ visits=2, value=0.70, ucb=2.09
├─ Next, we'll start adding numbers from le...
│ visits=1, value=0.70, ucb=1.87
├─ Find a place to write down the answer.
│ visits=0, value=0.00, ucb=inf
├─ Next, we can start adding the numbers di...
│ visits=0, value=0.00, ucb=inf
├─ 3. Let's do it together! Step 4: Countin...
│ visits=6, value=0.60, ucb=1.60
├─ Continue counting or moving on to the ne...
│ visits=2, value=0.60, ucb=1.93
├─ The next step would be to add the last t...
│ visits=1, value=0.60, ucb=1.77
├─ The next step would be to add the last n...
│ visits=0, value=0.00, ucb=inf
├─ Next, add the third number to reach the ...
│ visits=0, value=0.00, ucb=inf
├─ Next, let's add another number to comple...
│ visits=2, value=0.60, ucb=1.93
├─ Add another number.
│ visits=1, value=0.60, ucb=1.77
├─ 5. The final answer is 20.
│ visits=0, value=0.00, ucb=inf
├─ Next, let's count on from where we left ...
│ visits=0, value=0.00, ucb=inf
├─ It seems like there isn't a clear next s...
│ visits=1, value=0.60, ucb=2.49
├─ Next, we add the two numbers together. L...
│ visits=6, value=0.67, ucb=1.66
├─ The answer is:
│ visits=2, value=0.70, ucb=2.03
├─ To find the sum of 12 and 8, you can sim...
│ visits=1, value=0.70, ucb=1.87
├─ Next, what number should be added to the...
│ visits=0, value=0.00, ucb=inf
├─ Next, what is the sum of 12 and 8? To fi...
│ visits=0, value=0.00, ucb=inf
├─ The answer to the original problem is 20...
│ visits=2, value=0.70, ucb=2.03
├─ The answer to the original problem is 20...
│ visits=1, value=0.70, ucb=1.87
├─ The answer is 20.
│ visits=0, value=0.00, ucb=inf
├─ Next, we add the two numbers together. L...
│ visits=0, value=0.00, ucb=inf
├─ Next, let's perform the addition.
│ visits=1, value=0.60, ucb=2.49
MCTS with Learned Value Function¶
In AlphaGo (and AlphaZero), MCTS uses a neural network to:
Prior policy: Bias initial exploration toward promising moves
Value function: Replace rollouts with learned value estimates
For LLM reasoning, this means:
Use the LLM’s own probabilities as priors
Use a PRM or value head for evaluation
def puct_score(node: MCTSNode, prior: float, c_puct: float = 1.0) -> float:
"""
PUCT formula (Predictor + UCT) used in AlphaGo.
Incorporates a prior probability from the policy network.
PUCT(s, a) = Q(s, a) + c * P(a|s) * sqrt(N(s)) / (1 + N(s, a))
"""
if node.parent is None:
return node.value
exploitation = node.value
exploration = c_puct * prior * math.sqrt(node.parent.visits) / (1 + node.visits)
return exploitation + exploration
# Visualize UCB vs PUCT
visits = np.arange(1, 51)
parent_visits = 100
q_value = 0.6
c = 1.41
prior = 0.3 # Model thinks this action has 30% probability
ucb_scores = [q_value + c * math.sqrt(math.log(parent_visits) / v) for v in visits]
puct_scores = [q_value + c * prior * math.sqrt(parent_visits) / (1 + v) for v in visits]
plt.figure(figsize=(10, 6))
plt.plot(visits, ucb_scores, 'b-', label='UCB (no prior)', linewidth=2)
plt.plot(visits, puct_scores, 'r-', label=f'PUCT (prior={prior})', linewidth=2)
plt.axhline(y=q_value, color='gray', linestyle='--', label=f'Q-value = {q_value}')
plt.xlabel('Visits to this node', fontsize=12)
plt.ylabel('Selection score', fontsize=12)
plt.title('UCB vs PUCT: How Priors Affect Exploration', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("PUCT with high prior → more initial exploration of that action.")
print("PUCT with low prior → less exploration, need strong evidence to try.")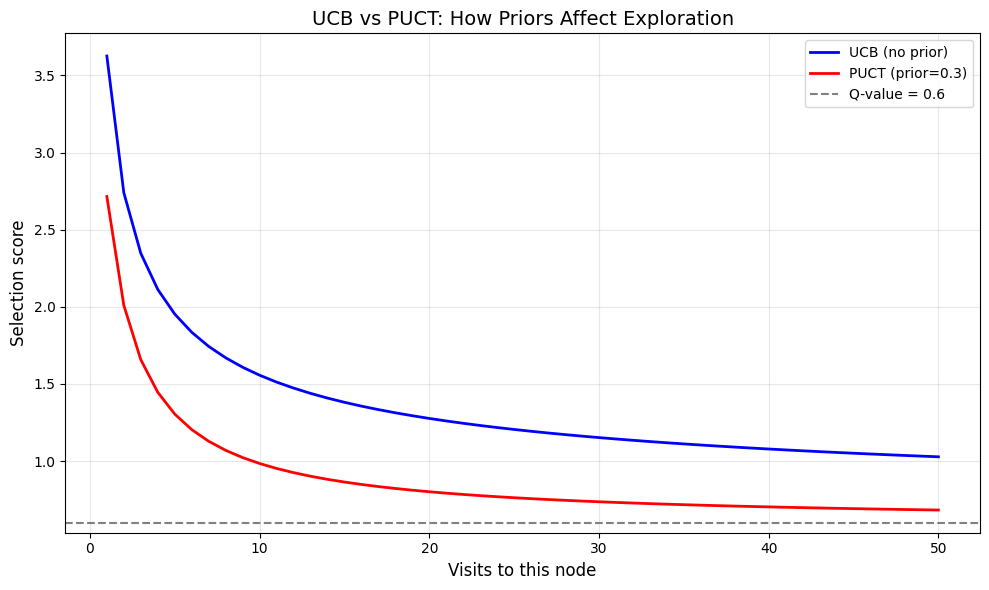
PUCT with high prior → more initial exploration of that action.
PUCT with low prior → less exploration, need strong evidence to try.
Benchmark: AlphaMath Results¶
From the AlphaMath paper (using MCTS for math reasoning):
| Method | GSM8K | MATH |
|---|---|---|
| Base model | 51.1% | 7.2% |
| + CoT | 58.3% | 12.5% |
| + MCTS (1 round) | 63.2% | 18.4% |
| + MCTS (3 rounds) | 78.8% | 41.2% |
MCTS + iterative refinement gets massive improvements!
What We’ve Learned¶
MCTS applies game-tree search to reasoning:
Select: Use UCB to balance exploration/exploitation
Expand: Generate possible next thoughts
Simulate: Evaluate with value function (or rollout)
Backpropagate: Update statistics up the tree
The UCB formula:
With priors (PUCT):
Key advantages over Best-of-N:
Explores promising paths more deeply
Abandons bad branches early
Uses compute more efficiently
Next up: Budget Forcing — controlling reasoning length with “Wait” tokens
