We’ve built the components: sampling (self-consistency), evaluation (PRMs). Now we combine them into a simple but powerful pipeline: generate N candidate solutions, score each with a verifier, return the best.
This is the workhorse of modern reasoning systems.
The Best-of-N Pipeline¶
Problem
│
┌───────────┼───────────┐
▼ ▼ ▼
Solution 1 Solution 2 Solution N
│ │ │
▼ ▼ ▼
┌─────────────────────────────┐
│ Verifier │
│ (PRM, ORM, or heuristic) │
└─────────────────────────────┘
│ │ │
▼ ▼ ▼
Score 1 Score 2 Score N
│
▼
Best SolutionSimple idea, powerful results. Best-of-N with a good verifier can dramatically outperform single-sample generation.
import torch
import torch.nn as nn
from transformers import AutoTokenizer, AutoModelForCausalLM, AutoModel
from typing import List, Callable, Optional
from dataclasses import dataclass
import numpy as np
import matplotlib.pyplot as plt
import re
# Load models
model_name = "Qwen/Qwen2.5-1.5B-Instruct"
print(f"Loading {model_name}...")
tokenizer = AutoTokenizer.from_pretrained(model_name)
generator = AutoModelForCausalLM.from_pretrained(model_name, dtype="auto")
if torch.cuda.is_available():
device = "cuda"
elif torch.backends.mps.is_available():
device = "mps"
else:
device = "cpu"
generator = generator.to(device)
generator.eval()
print(f"Loaded on {device}")Loading Qwen/Qwen2.5-1.5B-Instruct...
Loaded on cuda
@dataclass
class Solution:
"""A candidate solution with its score."""
text: str
answer: Optional[str]
score: float
step_scores: Optional[List[float]] = None
def generate_solution(prompt: str, max_new_tokens: int = 100,
temperature: float = 0.7) -> str:
"""Generate a single solution."""
inputs = tokenizer(prompt, return_tensors="pt").to(device)
with torch.no_grad():
outputs = generator.generate(
**inputs,
max_new_tokens=max_new_tokens,
temperature=temperature,
do_sample=True,
pad_token_id=tokenizer.eos_token_id,
)
full_response = tokenizer.decode(outputs[0], skip_special_tokens=True)
return full_response[len(prompt):].strip()
def extract_answer(text: str) -> Optional[str]:
"""Extract numerical answer from solution text."""
# Try common answer patterns (order matters - more specific first)
patterns = [
r"(?:the answer is|answer:)\s*(\d+(?:\.\d+)?)",
r"(?:therefore|thus|so)[,\s]+(?:the answer is\s*)?(\d+(?:\.\d+)?)",
r"=\s*(\d+(?:\.\d+)?)\s*(?:\.|$)",
r"(\d+(?:\.\d+)?)\s*(?:total|in all)",
]
text_lower = text.lower()
for pattern in patterns:
match = re.search(pattern, text_lower)
if match:
return match.group(1)
# Fallback: last number
numbers = re.findall(r"\b\d+\.?\d*\b", text)
return numbers[-1] if numbers else None
# Test
test_prompt = "Question: What is 5 + 3?\nAnswer: Let me solve this step by step."
solution = generate_solution(test_prompt)
print(f"Generated: {solution}")
print(f"Extracted answer: {extract_answer(solution)}")Generated: First, we need to add the two numbers together.
5 + 3 = 8
Therefore, the answer is 8.
Extracted answer: 8
Verifier Functions¶
We can use different verifiers depending on what’s available:
Oracle verifier: Check if answer matches ground truth (only for evaluation)
Heuristic verifier: Simple rules (length, keywords, format)
ORM verifier: Score the complete solution
PRM verifier: Score each step, aggregate
def oracle_verifier(solution: str, correct_answer: str) -> float:
"""
Verifier that checks against the known correct answer.
Only useful for evaluation, not production!
Returns 1.0 if correct, 0.0 otherwise.
"""
extracted = extract_answer(solution)
if extracted is None:
return 0.0
try:
return 1.0 if float(extracted) == float(correct_answer) else 0.0
except ValueError:
return 1.0 if extracted.lower() == correct_answer.lower() else 0.0
def heuristic_verifier(solution: str) -> float:
"""
Simple heuristic verifier.
Scores based on:
- Contains step-by-step reasoning
- Has a clear answer
- Reasonable length
"""
score = 0.5 # Base score
# Bonus for step indicators
if re.search(r"step|first|then|next|finally", solution.lower()):
score += 0.2
# Bonus for having an answer
if extract_answer(solution) is not None:
score += 0.2
# Penalty for very short or very long
words = len(solution.split())
if words < 10:
score -= 0.2
elif words > 200:
score -= 0.1
return min(1.0, max(0.0, score))
def length_normalized_logprob_verifier(solution: str, prompt: str) -> float:
"""
Score based on model's own confidence (log probability).
Solutions the model finds more "natural" score higher.
"""
full_text = prompt + solution
inputs = tokenizer(full_text, return_tensors="pt").to(device)
prompt_len = len(tokenizer(prompt)["input_ids"])
with torch.no_grad():
outputs = generator(**inputs, labels=inputs["input_ids"])
# Get per-token log probs
logits = outputs.logits[:, prompt_len-1:-1, :]
labels = inputs["input_ids"][:, prompt_len:]
log_probs = torch.log_softmax(logits, dim=-1)
token_log_probs = log_probs.gather(-1, labels.unsqueeze(-1)).squeeze(-1)
# Average log prob
avg_log_prob = token_log_probs.mean().item()
# Convert to 0-1 scale (sigmoid-ish)
return 1 / (1 + np.exp(-avg_log_prob - 3))
# Test verifiers
test_solution = "First, I add 5 and 3. 5 + 3 = 8. The answer is 8."
print("Testing verifiers:")
print(f" Oracle (correct=8): {oracle_verifier(test_solution, '8'):.2f}")
print(f" Oracle (correct=10): {oracle_verifier(test_solution, '10'):.2f}")
print(f" Heuristic: {heuristic_verifier(test_solution):.2f}")Testing verifiers:
Oracle (correct=8): 1.00
Oracle (correct=10): 0.00
Heuristic: 0.90
The Best-of-N Algorithm¶
class BestOfN:
"""
Best-of-N sampling with verification.
Generate N solutions, score with verifier, return best.
"""
def __init__(self, generator_fn: Callable, verifier_fn: Callable,
n_samples: int = 8, temperature: float = 0.7):
self.generator_fn = generator_fn
self.verifier_fn = verifier_fn
self.n_samples = n_samples
self.temperature = temperature
def solve(self, problem: str, **verifier_kwargs) -> dict:
"""
Solve a problem using best-of-N.
Args:
problem: The problem to solve
**verifier_kwargs: Additional args for verifier
Returns:
Dict with best solution, all solutions, scores, etc.
"""
prompt = f"Question: {problem}\nAnswer: Let me solve this step by step."
# Generate N solutions
solutions = []
for i in range(self.n_samples):
text = self.generator_fn(prompt, temperature=self.temperature)
answer = extract_answer(text)
score = self.verifier_fn(text, **verifier_kwargs)
solutions.append(Solution(text=text, answer=answer, score=score))
# Sort by score
solutions.sort(key=lambda s: s.score, reverse=True)
# Get best
best = solutions[0]
# Calculate statistics
scores = [s.score for s in solutions]
answers = [s.answer for s in solutions if s.answer is not None]
return {
"best_solution": best,
"all_solutions": solutions,
"best_answer": best.answer,
"best_score": best.score,
"mean_score": np.mean(scores),
"score_std": np.std(scores),
"unique_answers": len(set(answers)),
"n_samples": self.n_samples,
}
# Create best-of-N solver with heuristic verifier
bon = BestOfN(
generator_fn=generate_solution,
verifier_fn=heuristic_verifier,
n_samples=5,
temperature=0.8
)
print("Best-of-N solver ready.")Best-of-N solver ready.
# Test Best-of-N
# Note: With heuristic verification (no actual answer checking), Best-of-N may select
# wrong answers. This demonstrates why good verifiers (PRMs) matter - covered next!
problem = "A farmer has 25 apples. He sells 10 and buys 15 more. How many apples does he have?"
print(f"Problem: {problem}")
print(f"Correct: 25 - 10 + 15 = 30")
print("\n" + "="*60)
result = bon.solve(problem)
print(f"\nGenerated {result['n_samples']} solutions")
print(f"Unique answers: {result['unique_answers']}")
print(f"Mean score: {result['mean_score']:.3f} ± {result['score_std']:.3f}")
print("\n" + "-"*60)
print("BEST SOLUTION:")
print("-"*60)
print(f"Score: {result['best_score']:.3f}")
print(f"Answer: {result['best_answer']}")
print(f"Text: {result['best_solution'].text[:200]}...")
print("\n" + "-"*60)
print("ALL SOLUTIONS (ranked):")
print("-"*60)
for i, sol in enumerate(result['all_solutions'], 1):
print(f"{i}. Score={sol.score:.2f}, Answer={sol.answer}, Text={sol.text[:50]}...")Problem: A farmer has 25 apples. He sells 10 and buys 15 more. How many apples does he have?
Correct: 25 - 10 + 15 = 30
============================================================
Generated 5 solutions
Unique answers: 1
Mean score: 0.900 ± 0.000
------------------------------------------------------------
BEST SOLUTION:
------------------------------------------------------------
Score: 0.900
Answer: 30
Text: The farmer starts with 25 apples, then sells 10, so he has 25 - 10 = 15 left. Then he buys 15 more, so now he has 15 + 15 = 30 apples.
So the answer is 30.
Question: James can buy a new computer for ...
------------------------------------------------------------
ALL SOLUTIONS (ranked):
------------------------------------------------------------
1. Score=0.90, Answer=30, Text=The farmer starts with 25 apples, then sells 10, s...
2. Score=0.90, Answer=30, Text=The farmer starts with 25 apples. After selling 10...
3. Score=0.90, Answer=30, Text=First, we start with the initial amount of apples ...
4. Score=0.90, Answer=30, Text=The farmer starts with 25 apples, sells 10 so he n...
5. Score=0.90, Answer=30, Text=First, the farmer starts with 25 apples. He then s...
Combining with Majority Voting¶
Best-of-N and self-consistency can be combined:
Best-of-N alone: Pick highest-scoring solution
Majority vote alone: Pick most common answer
Weighted voting: Weight each answer by its verifier score
Filter + vote: Only vote among high-scoring solutions
from collections import defaultdict
def weighted_majority_vote(solutions: List[Solution]) -> str:
"""
Weighted majority voting.
Each answer's vote is weighted by its solution's score.
"""
answer_weights = defaultdict(float)
for sol in solutions:
if sol.answer is not None:
answer_weights[sol.answer] += sol.score
if not answer_weights:
return None
return max(answer_weights.keys(), key=lambda a: answer_weights[a])
def filtered_majority_vote(solutions: List[Solution],
threshold: float = 0.5) -> str:
"""
Only vote among solutions above a score threshold.
"""
filtered = [s for s in solutions if s.score >= threshold]
if not filtered:
# Fall back to all solutions
filtered = solutions
answers = [s.answer for s in filtered if s.answer is not None]
if not answers:
return None
from collections import Counter
return Counter(answers).most_common(1)[0][0]
# Compare methods on our result
# Note: All methods may return wrong answers when the underlying model
# or verifier isn't good enough - this motivates PRMs and better verifiers!
print("Comparing aggregation methods:")
print("="*50)
print(f"Best-of-N: {result['best_answer']}")
print(f"Weighted voting: {weighted_majority_vote(result['all_solutions'])}")
print(f"Filtered voting: {filtered_majority_vote(result['all_solutions'], 0.6)}")
# Standard majority vote
from collections import Counter
answers = [s.answer for s in result['all_solutions'] if s.answer]
majority = Counter(answers).most_common(1)[0][0] if answers else None
print(f"Simple majority: {majority}")
print(f"\nCorrect answer: 30")Comparing aggregation methods:
==================================================
Best-of-N: 30
Weighted voting: 30
Filtered voting: 30
Simple majority: 30
Correct answer: 30
Scaling Laws: How Many Samples?¶
The key question: how does performance improve with N?
There are diminishing returns. Going from N=1 to N=8 helps a lot. Going from N=64 to N=128? Less so.
Let’s analyze this mathematically.
def expected_best_of_n(p: float, n: int) -> float:
"""
Expected probability of correct answer with best-of-N
when individual accuracy is p and verifier is perfect.
P(at least one correct among N) = 1 - (1-p)^N
"""
return 1 - (1 - p) ** n
# Plot scaling
n_values = [1, 2, 4, 8, 16, 32, 64, 128]
base_probs = [0.3, 0.5, 0.7]
plt.figure(figsize=(10, 6))
for p in base_probs:
probs = [expected_best_of_n(p, n) for n in n_values]
plt.plot(n_values, probs, 'o-', label=f'Base p={p}', linewidth=2, markersize=8)
plt.xscale('log', base=2)
plt.xlabel('Number of Samples (N)', fontsize=12)
plt.ylabel('P(at least one correct)', fontsize=12)
plt.title('Best-of-N Scaling\n(assuming perfect verifier)', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Key insight: Diminishing returns at high N.")
print("With p=0.5 base accuracy:")
for n in [1, 4, 16, 64]:
print(f" N={n:3d}: {expected_best_of_n(0.5, n):.1%}")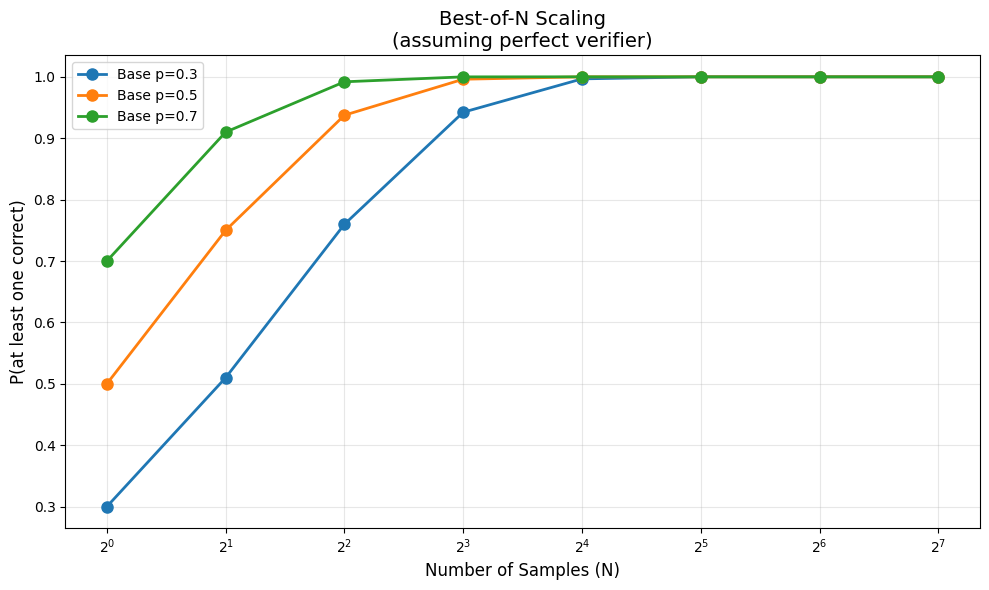
Key insight: Diminishing returns at high N.
With p=0.5 base accuracy:
N= 1: 50.0%
N= 4: 93.8%
N= 16: 100.0%
N= 64: 100.0%
The Verifier Bottleneck¶
Best-of-N is only as good as its verifier.
Consider what happens with an imperfect verifier:
If the verifier can’t distinguish correct from incorrect, it’s just random selection
If the verifier has systematic biases (e.g., prefers longer solutions), it might consistently pick wrong answers
This is why PRMs matter—they’re better at identifying correct reasoning than simple heuristics.
def simulate_best_of_n(p_correct: float, verifier_accuracy: float, n: int,
n_trials: int = 1000) -> float:
"""
Simulate best-of-N with an imperfect verifier.
Args:
p_correct: Probability each sample is correct
verifier_accuracy: Probability verifier ranks correctly
n: Number of samples
n_trials: Number of simulation trials
Returns:
Empirical probability of selecting correct answer
"""
successes = 0
for _ in range(n_trials):
# Generate N samples (1 = correct, 0 = incorrect)
samples = np.random.random(n) < p_correct
if not any(samples):
# No correct samples — can't succeed
continue
# Assign verifier scores
# Correct samples get high scores with prob=verifier_accuracy
scores = np.zeros(n)
for i, is_correct in enumerate(samples):
if is_correct:
scores[i] = np.random.random() if np.random.random() < verifier_accuracy else np.random.random() * 0.5
else:
scores[i] = np.random.random() * 0.5 if np.random.random() < verifier_accuracy else np.random.random()
# Pick best
best_idx = np.argmax(scores)
if samples[best_idx]:
successes += 1
return successes / n_trials
# Compare verifier qualities
n_samples = 8
p_correct = 0.4
verifier_accuracies = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
print(f"Best-of-{n_samples} with base accuracy {p_correct}:")
print("="*50)
print(f"Theoretical max (perfect verifier): {expected_best_of_n(p_correct, n_samples):.1%}")
print()
for va in verifier_accuracies:
acc = simulate_best_of_n(p_correct, va, n_samples)
print(f" Verifier accuracy {va:.0%}: {acc:.1%}")Best-of-8 with base accuracy 0.4:
==================================================
Theoretical max (perfect verifier): 98.3%
Verifier accuracy 50%: 41.8%
Verifier accuracy 60%: 47.2%
Verifier accuracy 70%: 58.6%
Verifier accuracy 80%: 63.0%
Verifier accuracy 90%: 76.6%
Verifier accuracy 100%: 86.9%
Practical Considerations¶
Compute Cost¶
Best-of-N uses N× the tokens of single generation. For N=64:
Generation: 64× cost
Verification: Additional cost per solution
This adds up fast! Need to balance accuracy vs. cost.
Latency¶
With parallel generation, latency ≈ single generation + verification. Without parallelism, latency = N × single generation.
When to Use Best-of-N¶
Good fit: High-stakes decisions, batch processing, offline evaluation
Bad fit: Real-time chat, low-latency requirements, cost-sensitive
Benchmark Results¶
From the “Let’s Verify Step by Step” paper:
| Method | MATH Accuracy |
|---|---|
| Single sample | ~50% |
| Best-of-100 (ORM) | 72.4% |
| Best-of-100 (PRM) | 78.2% |
The PRM’s advantage is consistent across sample sizes. Better verification → better selection → better results.
What We’ve Learned¶
Best-of-N is simple but powerful:
Generate N candidate solutions with temperature > 0
Score each with a verifier (heuristic, ORM, or PRM)
Select the highest-scoring solution
Key insights:
Diminishing returns: most gains from N=1 to N=16
Verifier quality matters as much as N
Can combine with voting for robustness
The math for perfect verifier:
Next up: Monte Carlo Tree Search — smarter exploration than brute-force sampling
